Venezolano descubre patrón inédito en los números primos conocidos

Venezolano descubre patrón inédito en los números primos conocidos

13/02/2019

A principios del segundo trimestre del año 2018, el venezolano Ardly Crespo licenciado en Administración Comercial en la Universidad Central de Venezuela, presentó a un conjunto de matemáticos de la misma universidad, un trabajo donde al parecer, muestra un patrón presente en los números primos conocidos. A pesar de que el trabajo no incluye pruebas soportadas por fórmulas matemáticas, fue realizada la verificación del procedimiento que plantea, y efectivamente arroja los resultados esperados en los números primos en los que fue analizado el procedimiento.

Basándose en lo que hace un tiempo se conoce como la Matemática Vorticial (MV) presentada por Marko Rodin; Ardly Crespo muestra un procedimiento que afirma, servirá como punto de partida para próximos descubrimientos que permitirán determinar la “distribución de los números primos entre los números naturales”. Además, indica que tomando en cuenta los conceptos presentados por la Matemática Vorticial (MV), sobre las cualidades de los números (de acuerdo a la MV todos los números naturales tienen nueve cualidades), se puede construir una tabla donde puede verificarse,  que existen tres rangos o grupos de infinitos números, donde no se encontrarán números primos, a saber los números que posean las cualidades 3, 6 y 9 a excepción del número 3, afirmación que según el autor podrían corroborar posteriormente con especialistas en el área. En MV para determinar la cualidad de un número, deben sumarse sucesivamente los dígitos que conforman a dicho número, hasta obtener un número de un solo dígito; ejemplo, si tomamos el número primo 1.723, realizamos las sumas sucesivas para obtener su cualidad: 1 + 7 + 2 + 3 = 13, luego sumamos 1 + 3 = 4 lo que nos muestra que el número primo 1.723 tiene como cualidad 4. Lo anterior indica, que al tener nueve grupos de infinitos números, ya tenemos tres grupos, afirma Ardly Crespo de acuerdo a su investigación, que poseen las cualidades 3, 6 y 9 donde no encontraremos ningún primo a excepción del número primo 3, que es el único número primo con cualidad 3 y está dentro de los grupos antes mencionados.

Lo anterior, nos lleva a un conjunto de seis (6) grupos de infinitos números naturales incluidos dentro de las cualidades 1, 2, 4, 5, 7 y 8, dentro de los cuales, solo encontraremos números primos que terminan en los dígitos 1, 3, 7 y 9, puesto que los números primos como se sabe, presentan la característica de ser números impares, a excepción del número 2 que es el único número primo par.

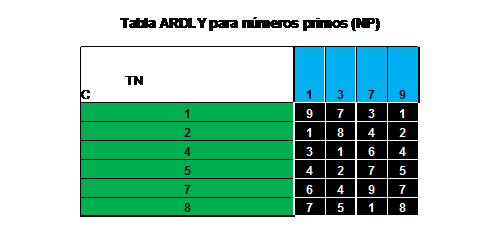
Toda la explicación preliminar de acuerdo al autor, era necesaria, primero para entender cómo se obtienen las cualidades de los números primos, y segundo, para darle entrada al procedimiento que plantea a continuación. Ya conocidas las cualidades donde podremos encontrar números primos, a saber las cualidades (1, 2, 4, 5, 7 y 8) y sabiendo que dentro de cada una de ellas solo encontraremos números terminados en los dígitos (1, 3 , 7 y 9), el autor presenta una tabla la cual ha llamado “Tabla Ardly para números primos NP”, con la cual afirma, puede determinar de acuerdo al número con el cual termina un número primo, cuánto debe dar la suma sucesiva de sus dígitos a la izquierda del último dígito, el cual no es incluido en dicha suma, y como resultado da un número de un dígito. La tabla tal como una matriz, presenta un cruce entre las cualidades colocadas como filas en la tabla (1, 2, 4, 5, 7, y 8) contra la terminación del número colocada como las columnas en la tabla (1, 3, 7 y 9). Al realizar este cruce, se obtiene un número en la intercepción de ambas, que debe ser igual a la suma sucesiva de los dígitos mencionada anteriormente donde se obtiene un resultado de un dígito.

Si aplicamos el procedimiento al número primo mencionado arriba 1.723 verificamos lo siguiente:

Cualidad = 1+ 7 + 2 + 3 : 13 = 1 + 3 : 4   Cualidad 4

Terminal del número 3

Por último sumamos los dígitos a la izquierda del número 3 sin incluir en la suma a éste:

1 + 7 + 2 : 10 = 1 + 0 : 1   Resultado 1

Al cruzar en la tabla la cualidad 4 con el terminal del número 3, verificamos que su resultado debe ser 1 como se obtuvo.

Este procedimiento ha sido probado en una cantidad representativa de número primos, obteniéndose los resultados presentados en la tabla, pero su autor pide a la comunidad matemática sea probado en los últimos diez números primos descubiertos.

Si bien es cierto que el trabajo presentado por el venezolano Ardly Crespo, no muestra la rigurosidad matemática en cuanto a demostraciones con fórmulas que prueben, y den muestra que se ha servido de demostraciones por inducción matemática, también es cierto, que el procedimiento deja ver que existen formas que llevadas a la práctica, nos muestran detalles que la matemática convencional no ha podido demostrar hasta ahora, o por lo menos, servirán para estudios posteriores que ayuden a vislumbrar más cosas ocultas sobre los siempre misteriosos números primos.

P.G. Casozzo: “…, la más crítica necesidad en matemáticas son las nuevas ideas creativas, y éstas pueden proceder de cualquiera”.

A continuación la “Tabla Ardly para números primos NP”

https://www.mixtecnico.net/wp-content/uploads/2019/02/Cuadro-Tabla-Ardly-NP.gif

Para observaciones o compartir criterios en cuanto a lo anterior pueden escribir al autor a:

[email protected] o [email protected].